ЗАДАЧА 25

Фирма пробует различные стратегии организации обслуживания населения (в январе-мае), получая за каждую из них в соответствующем периоде определенную прибыль в млн. руб. (см. платежную матрицу А). Необходимо определить наилучшую стратегию (стратегии) фирмы на будущее:

1. придерживаясь исключительно определенной тактики, использованной в предыдущие месяцы и рассчитывая на логичное поведение клиентов

2. сочетая в будущем различные стратегии предшествующих месяцев, также рассчитывая на логичное поведение клиентов

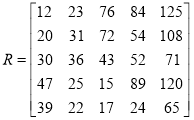
3. предполагая, что клиенты в будущем поведут себя непредсказуемо (матрица рисков R)

  

Решение.

      Определим седловой элемент:

    

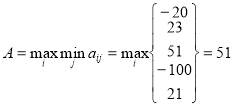
  Матрица не имеет седлового элемента:

А  ≠ В           51≤ v ≤ 69

1.                     В данном случае необходимо выбрать одну из предлагаемых пяти стратегий. Т. е. решение матричной игры будет представлено в чистых стратегиях.

Найдем оптимальную стратегию  по критерию Лапласа.

n

Аi = mах1/n  Aij

i             j=1

А1 = (256 + 235 + 158 + 64 – 20)/5 = 138,6;

А2 = (148 + 124 + 76 + 122 + 23)/5 = 98,6;

А3 = (102 + 123 + 96 + 88 + 51)/5  = 92;

А4 = (89 + 105 + 171 + 36 – 100)/5  = 60,2;

А5 = (21 + 72 + 127 + 104 + 69)/5  = 78,6.

Оптимальной является  стратегия А1.

Если ориентироваться на выбор одной из стратегий и на логичное поведение покупателей оптимальной является стратегия А1.

2.               Если необходимо в будущем выбрать комбинацию стратегий, то необходимо составить и решить пару двойственных задач. Избавляемся от отрицательных элементов в платежной матрице, для этого прибавляем к каждому элементу число 100. В результате получим:

Таблица 3.1.

356	335	258	164	80
248	224	176	222	123
202	223	196	188	151
189	205	271	136	0
121	172	227	204	169

Составляем пару двойственных задач.

Для игрока А:

F = X1 + X2 + X3 + X4 + X5    (min)

356X1 + 248X2 + 202X3 + 189X4 +  121X5 ≥1,

335X1 + 224X2 + 223X3 + 205X4 +  172X5 ≥1,

258X1 + 176X2 +  196X3 +271X4 + 227X5 ≥1,

 164X1 + 222X2 + 188X3 +136X4 + 204X5 ≥1,

  80X1 + 123X2 + 151X3  +   0X4 +  169X5 ≥1,

Хj  ≥0

Для игрока В:

Z = Y1 + Y2 + Y3 + Y4 + Y5   (max)

 

356Y1 + 335Y2 + 258Y3 +  164Y4 -  120Y5 ≤1,

248Y1 + 224Y2 + 176Y3 + 222Y4 +   33Y5 ≤1,

202Y1 + 223Y2 + 196Y3 +  188Y4 +  151Y5 ≤1,

189Y1 + 205Y2 + 271Y3 + 136Y4  +     0Y5 ≤1,

121Y1 + 172Y2 + 227Y3 +  204Y4 +  169Y5 ≤1,

Yi≥0

 

Решим полученную пару двойственных задач с помощью Excel. Создаем модель задачи и заполняем диалоговое окно «Поиск решения».

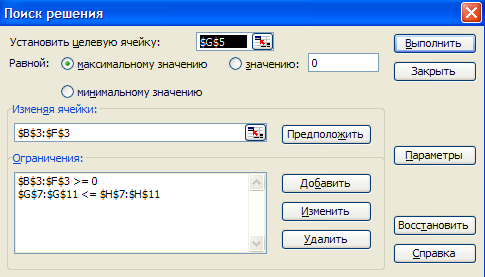
Рис. 3.1.

В результате получим (Рис. 3.2).

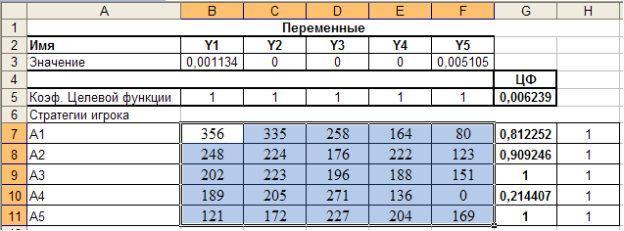
Рис. 3.2.

Таблица 3.2. Отчет по устойчивости.

Изменяемые ячейки
			Результ.	Нормир.
	Ячейка	Имя	значение	градиент
	$B$3	Значение Y1	0,00113443	0
	$C$3	Значение Y2	0	-0,227453205
	$D$3	Значение Y3	0	-0,322556249
	$E$3	Значение Y4	0	-0,224428058
	$F$3	Значение Y5	0,005104935	0
Ограничения
			Результ.	Лагранжа
	Ячейка	Имя	значение	Множитель
	$G$7	А1 ЦФ	0,812251843	0
	$G$8	А2 ЦФ	0,909245604	0
	$G$9	А3 ЦФ	1	0,003025147
	$G$10	А4 ЦФ	0,21440726	0
	$G$11	А5 ЦФ	1	0,003214218

 

Используя отчет по устойчивости записываем решение для игрока А: Х* = (0; 0; 0,003; 0; 0,0032).

Находим оптимальную смешанную стратегию для игрока А:

     p1* = v · X1* = 0∙(1/0,0062) = 0;  p2* = v · X2* =0;  p3* = v · X3* =0,485;   p4* = v · X4* = 0;    p5* = v · X5* = 0,515.

Следовательно, в будущем  на 48,5% фирма должна использовать стратегию А3 и на 51,5% стратегию А5.

3.                В случае когда клиенту в будущем поведут себя непредсказуемо, воспользуемся критерием Сэвиджа.

Аi = min max rij=min(125, 108, 71, 120, 65) = 65
i         j

По критерию Сэвиджа  оптимальной является     5-я    стратегия.