Примеры решения задач по рынку ценных бумаг - опционы.
Задание на семинар 4
Задание 1
Вычислите цену трехмесячного европейского опциона на продажу бездивидендной акции с ценой исполнения, равной 50 долл., если текущая цена акции равна 50 долл., безрисковая процентная ставка – 10% годовых, а волатильность – 30% в год.
Решение
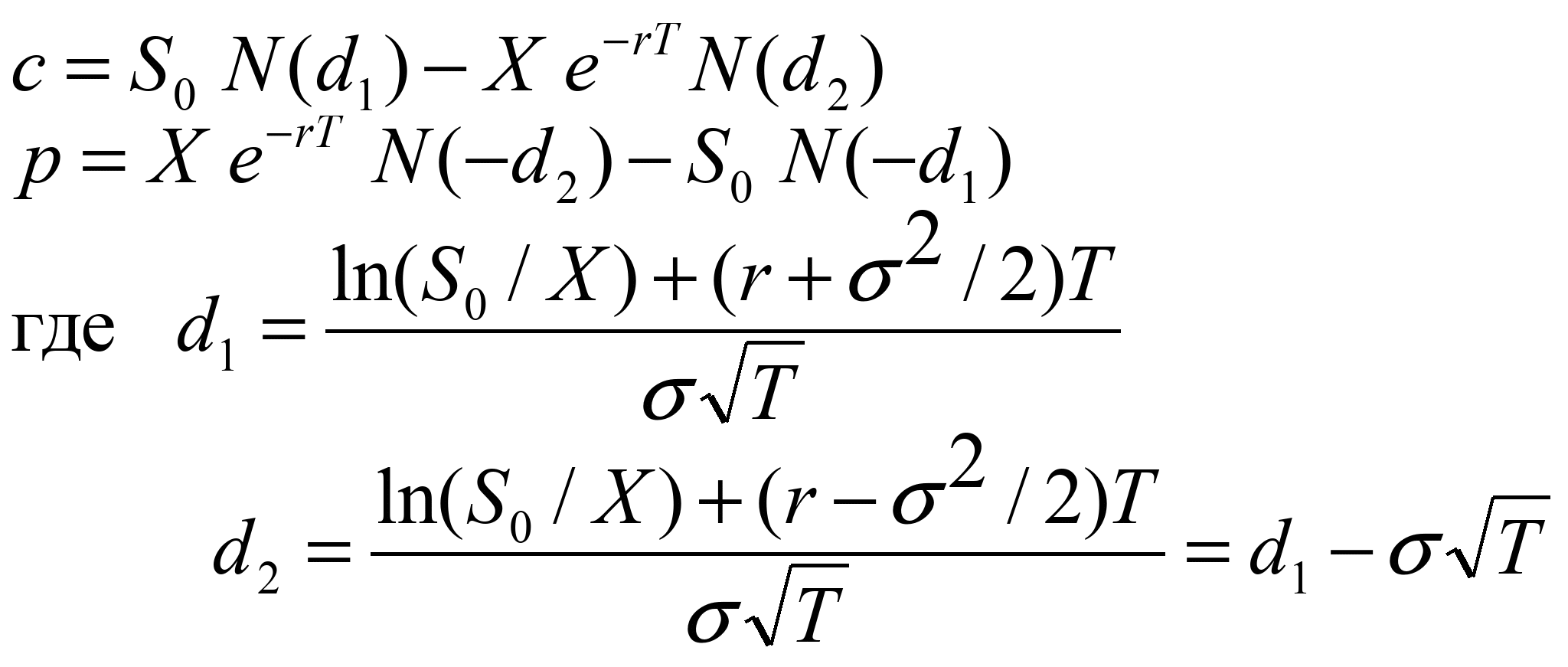
Из условий задачи следует, что S0 = 50 долл., K = 50 долл., r = 0,1, σ = 0,3, Т = 0,25.
Следовательно:
|
d1 = |
0,24167 |
|
d2 = |
0,09167 |
|
N(d1) = |
0,59548 |
|
N(d2) = |
0,53652 |
|
N(-d1) = |
0,40452 |
|
N(-d2) = |
0,46348 |
|
c = |
3,61045 |
|
p = |
2,37594 |
Задание 2
Цена акции подчиняется законам геометрического броуновского движения с ожидаемой доходностью, равной 16%, и волатильностью, равной 35%. Текущая цена акции равна 38 долл. Безрисковая процентная ставка 5%.
-
Какова вероятность того, что шестимесячный европейский опцион на покупку акций с ценой исполнения, равной 40 долл., будет исполнен?
-
Какова вероятность того, что будет исполнен европейский опцион на продажу акций с такой же ценой исполнения и таким же сроком действия?
-
Вычислите цены этих опционов с помощью модели Блэка-Шоулза.
Решение
В соответствии со свойствами геометрического броуновского движения:
![]()
Предположим, что цена акции через шесть месяцев (Т=0,5) составит S0,5. Тогда:
![]() ̴
̴ ![]()
![]() ̴ N(3,687; 0,247)
̴ N(3,687; 0,247)
ln40 = 3,689.
Поскольку вероятность того, что опцион Call будет исполнен равна вероятности того, что S0,5 (т.е. цена акции через полгода) будет не менее 40, то:
![]() , где
, где
ɸ - кумулятивное стандартное нормальное распределение.
2. Вероятность того, что будет исполнен европейский опцион на продажу равна вероятности того, что цена акции будет меньше 40 долл., т.е. вероятности того, что опцион Call не будет исполнен. Таким образом, эта вероятность составит:
1 - 0,5031 = 0,4969.
3. Цены опционов рассчитываются по формулам:
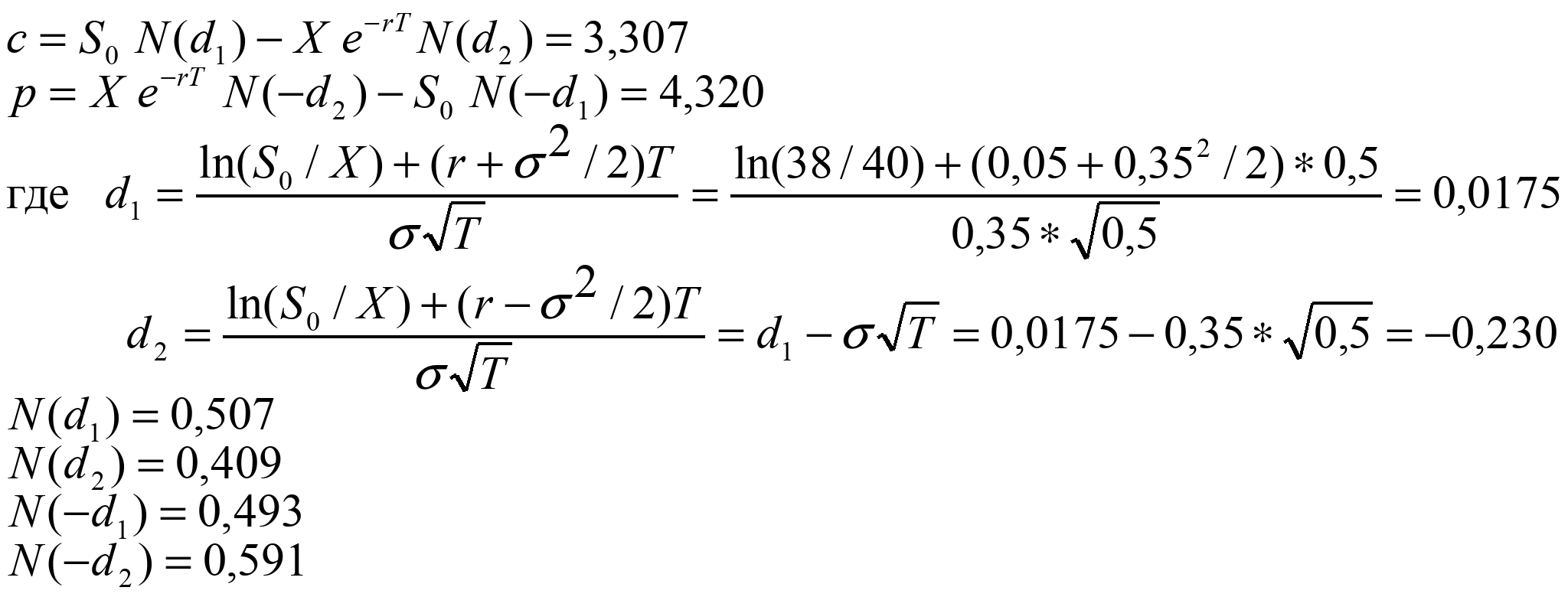
Задание 3
Чему равна цена трехмесячного европейского опциона на покупку бездивидендной акции, если ее цена равна 52 долл., цена исполнения – 50 долл., безрисковая процентная ставка – 12% годовых, а волатильность – 30% в год?
Решение
|
d1 = |
0,53647 |
|
d2 = |
0,38647 |
|
N(d1) = |
0,70418 |
|
N(d2) = |
0,65043 |
|
N(-d1) = |
0,29582 |
|
N(-d2) = |
0,34957 |
|
c = |
5,05739 |
|
p = |
1,57966 |
Задание 4
Рыночная цена на покупку бездивидендной акции равна 2,5 долл. Цена акции равна 15 долл., цена исполнения – 13 долл., срок до завершения – три месяца, а безрисковая процентная ставка – 5% годовых. Чему равна подразумеваемая волатильность?
Решение
Используя формулы Блэка-Шоулза, подбираем величину стандартного отклонения, приводящую при заданных условиях к цене опциона Call, равной 2,5 долл.
Получаем 39,64%.
Задание 5
Докажите, что формулы Блэка-Шоулза для вычисления стоимости опционов Call и Put удовлетворяют условию их паритета.
Задание 6
Предположим, что цена акции Sn подчиняется законам геометрического броуновского движения с математическим ожиданием μ и волатильностью σ.
dS = μSdt + σSdz
Каким процессом описывается переменная Sn?
Решение
Если G(S,t) = Sn, то:
![]()
Используя лемму Ито:
![]()
Мы знаем, что dS = μSdt + σSdz. То есть, a = μS, b = σS. Следовательно:
![]()
откуда следует:
![]()
Поскольку G(S,t) = Sn , то можно записать:
![]()
Следовательно G подчиняется геометрическому броуновскому движению с ожидаемой доходностью ![]() и волатильностью nσ.
и волатильностью nσ.
