Пример решения задачи - игра, графическим методом

Оптимизация мощности ателье.

Ателье по пошиву одежды рассчитано на выполнение не более 8 тыс. заявок в год. Будем считать, что поток заявок выражается цифрами 6, 8 тыс. в год. Накопленный опыт аналогичных предприятий показывает, что прибыль от выполнения одной заявки составляет 8 ден. ед., а потери, вызванные отказом из-за недостатка мощностей, оцениваются в 5 ден. ед., а убытки от простоя специалистов и оборудования при отсутствии заявок обходятся в 6 ден. ед. в расчете на каждую заявку.

1. Придать описанной ситуации игровую схему, установить характер игры и выявить ее
участников, указать возможные чистые стратегии сторон;

2. Составить платежную матрицу (матрицу затрат).

3.  Решить задачу сведением ее к задаче линейного программирования и решить её графическим способом (т.е. найти оптимальные стратегии игроков и цену игры). Дать рекомендации о мощности ателье.

Решение.

1. Одним из участников рассматриваемой в задаче ситуации являет­ся руководство предприятия, озабоченное необходимостью выполнения опреде­ленного количества заявок. Если описанной ситуации придать игровую схему, то руководство ателье выступает в ней в качестве сознательного игро­ка А, заинтересованного в максимизации прибыли от выполнения заказов . Вторым участником является природа - совокупность объективных факто­ров (П), которая реализует свои состояния по присущим ей законам. Такого рода ситуация представляется типичной для стратегической игры.

Рассчитывая количество заявок, руководство предприятия может ориентироваться на величины: 6 тыс. ед. (первая чистая стратегия А1), либо 8 тыс. ед. (вторая чистая стратегия А2).

Природа (совокупность объективных неопределенных факторов) мо­жет реализовать состояния П1, П2, необходимое количество заявок 6, 8 тыс. ед. соответственно.

Таким образом, платежная матрица статистической игры будет иметь размерность 2х2.

2. Платежная матрица игры представлена в табл. 2.1.

Таблица 2.1

	П1=6	П2=8	тin  aj
A1=6	48	48-2·5=38	18
А2=8	48-2·6=36	64	36

При расчете элементов матрицы учтена прибыль за вычетом дополнительных за­трат, связанных с недостатком мощностей, а также с убытком от простоя . Заметим, что в теории игр элементы  aij  обыч­но называются выигрышами игрока A, а наилучшей для  А считается страте­гия, при которой выигрыш максимизируется .

Рассмотрим ситуацию (а1;П2), т.е. случай, когда не хватает  мощности на 2 тыс. ед. при этом прибыль составит 64-2·5=54 . Так что «выигрыш» в этом случае равен 54 и т. д.

В ситуации (А2;П1) мощность превысит потребности на 8-6=2 (вес.  ед.). Поэтому затраты связанные с простоем составят 2·6=12 (ед.). Следовательно, a21 = 48-2·6=36.

Рассуждая аналогично, находим и остальные элементы платежной матрицы.

Определим седловой элемент:

    

Матрица не имеет седлового элемента т.к.       А  ≠ В           36 ≤ v ≤ 48

3. Для определения оптимальных стратегий игроков по платежной матрице составляем пару двойственных задач.

Для игрока А:

f =  Х1  + Х2  (min)                        

            48Х1 +36Х2 ≥1

            38Х1 +64Х2  ≥1                    (1)

                       Хj  ≥0   (j=1,2)                                       

Для игрока В:

  φ = Y1 + Y2  (max)     

      48Y1 + 38Y2  ≤ 1     

      36Y1 + 64Y2  ≤ 1                           (2)

        Yi  ≥0   (i=1,2)   

 

Решим задачу для игрока А графическим способом.

Строим прямые:

48Х1 +36Х2 =1  (I) по точкам (1/48, 0) и (0, 1/36)

38Х1 +64Х2  =1    (II) по точкам (1/38, 0) и (0, 1/64)

Долее определяем область допустимых решений. На рисунке 2.1 выделена граница области    допустимых решений. Разрешающая прямая     fmin, перпендикулярная вектору целевой функции 0,03С, засекает область в точке А, найдем координаты     точки А, решив систему уравнений:

48Х1 +36Х2 =1    (16)

38Х1 +64Х2  =1    (-9)

Умножаем первое уравнение на 16, а второе на (-9), складывая, получаем:

426Х1=7, откуда Х1*=7/426

Х2* = (1 - 48∙(7/426) )/36= 5/852

fmin  = 7/426 + 5/852 = 19/852

Цена игры: v = 1/fmin = 852/19.

Тогда оптимальные стратегии для игрока А:

Р1* = v∙X1* = (852/19)∙(7/426) = 14/19;

Р1* = v∙X2* = (852/19)∙(5/852) = 5/19.

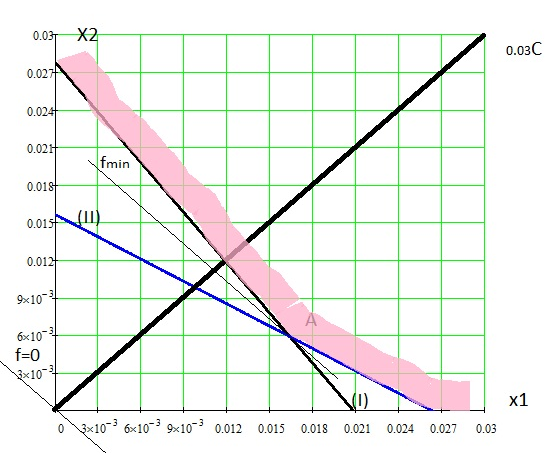
Рис. 2.1

Следовательно, руководству надо ориентироваться на (6000∙14+8000∙5)/19 = 6526 заявок в год.

Решим задачу для игрока В. Так как неравенства в задаче для игрока А при оптимальном решении  превращаются в строгие равенства, то оптимальное решение, найдем, решив систему:

48Y1 + 38Y2 =1      (-3)

36Y1 + 64Y2  =1      (4)     

Умножаем первое уравнение на (-3), а второе на 4, складывая, получаем:

142Y2=1, откуда Y2*= 1/142 = 6/852

Y1* = (1 - 38∙(1/142))/48 = 104/(142∙48) = 13/852

fmin  = 13/852 + 6/852 = 19/852

Цена игры: v = 1/ φ max = 852/19.

Тогда оптимальные стратегии для игрока B:

Q1* = v∙Y1* = (852/19)∙(13/852) = 13/19;

Q1* = v∙Y2* = (852/19)∙(6/852) = 6/19.