Пример решения задачи -графический метод линейного анализа.

Применяя графический метод линейного анализа, найти оптимальное решение для оснащения оборудованием новой лаборатории по проведению сертификационных испытаний сточных вод на содержание 12 нормируемых опасных веществ.

  На основании заводской лаборатории импортным оборудованием, не смотря на экономический кризис, выделено А долларов. Предполагается закупить измерительные приборы двух типов. Первый из них предназначен для экспресс-анализа по всей группе опасных веществ, его стоимость равна А1. Второй- может вести анализ лишь последовательно по одному элементу, но его цена А2 существенно меньше. Время, затрачиваемое на пробоподготовку и выполнение анализа одинаково и равно Т. Годовой ресурс времени на проведение измерений составляет Р=600 часов на каждый прибор (учесть при расчете количества измерений, выполняемых каждым прибором за год). Стоимость одного анализа на первом приборе(по 12 веществам сразу) составляет В1 долларов, на втором( по одному веществу)-В2..Нормируемая цена, которую платит лаборатории заказчик, анализа по одному опасному веществу составляет Вн. Считая, что иных доходов и расходов нет, оптимизировать прибыль при полной загрузке лаборатории.

 

Вариант	ПЕРЕМЕННЫЕ
	А	А1	А2	В1	В2	Вн	Т
4	180000	80000	10000	100	20	200	4

Решение.

Обозначим через Х1 и Х2 – количество приборов типа 1 и 2 соответственно, планируемых к закупке.

Тогда ограничение по бюджету закупки запишется в виде:

80000∙Х1 + 10000∙Х2  180000.     (1)

Определяем количество измерений, которое может произвести каждый  из приборов за год  Р/Т = 600/4 = 150 раз.

Так как первый вид приборов может произвести за одно измерение анализ по 12 веществам, то цена заказчика составит 12∙200 = 2400 д. е. С учетом стоимости анализа получим: 2400 – 100 = 2300 д.е. За год эта сумма составит 2300∙150 = 345000 д. е. Здесь, 150 – число измерений в год, выполняемых одним прибором. Вычитая из полученной суммы стоимость прибора получаем величину годовой чистой прибыли,  получаемую при эксплуатации прибора первого вида П1 = 345000 – 80000 = 265000 д. е.

Аналогично находим величину годовой чистой прибыли, получаемую в результате эксплуатации прибора 2-го типа. Здесь следует учесть, что данный тип прибора проводит анализ только по одному типу веществ. П2 = (200∙1 – 20)∙150 – 10000 = 17000 д. е.

В результате получим целевую функцию, характеризующую чистую прибыль, полученную в результате  эксплуатации  закупленных приборов:

F = 265 000 ∙X1 + 17 000∙X2 → max       (2)

Так же по смыслу задачи переменные Х1 и Х2 не могут выражаться отрицательными числами:

Х1 0; Х2 0                                                (3)

Математически задача сводится к отысканию таких значений Х1*, Х2*, которые удовлетворяли бы ограничениям (1) и (3) и доставляли бы максимум линейной функции (2).

Решим полученную задачу графическим способом.

Полагая неравенства (1) и (3) равенствами строим полученные прямые. Затем определяем область допустимых значений. Треугольник АВС является областью допустимых значений. Затем строим вектор С/17000 = (15,588; 1). Разрешающая прямая, перпендикулярная вектору С/17000 засекает область АВС в точке А. Её координаты Х1= 2,25; Х2 = 0.

Но значение Х2 должно быть целым. Следовательно, надо закупить два прибора 1-го вида, а на оставшуюся сумму докупить приборы второго типа. Определим остаток суммы 180000 – 2 ∙80000 = 20000 д. е. Количество приборов 2-го типа 20000/10000 = 2.

Следовательно, необходимо закупить два  прибора первого типа, и два прибора второго типа, прибыль при  этом будет максимальной и составит 2∙ 265 000 + 2∙ 17 000 = 564 000 д. е.

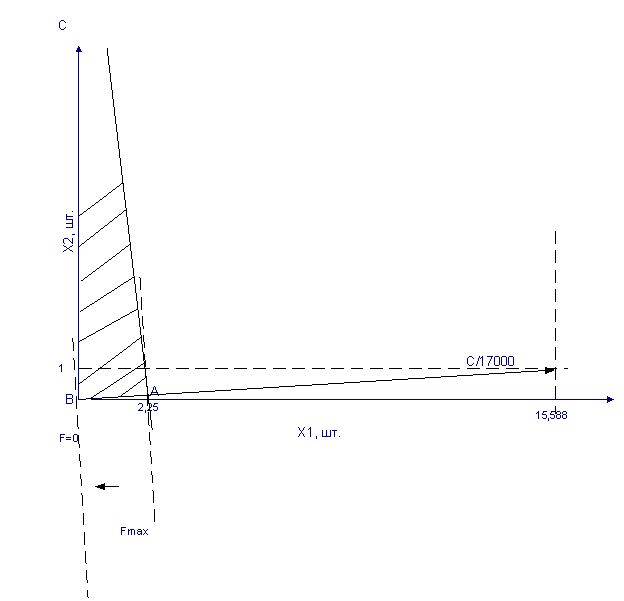Рис. 1.