Пример решения задачи дробно-линейного программирования.

Решить задачу дробно-линейного программирования:

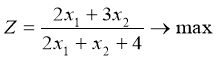
4X1 + X2 ≤ 10,

 X1 + 4X2≤ 10,

X1≥0, X2≥0.

Решение.

Сведем данную задачу к задаче линейного программирования. Сначала введем дополнительные переменные, чтобы привести задачу к каноническому виду:

4X1  + X2 + Х3 = 10,

 X1 + 4X2  + Х4 = 10,

X1≥0, X2≥0, X3≥0, X4≥0.

 

Обозначим , yj = y0∙Xj, j=1,…, 4

Тогда задача примет вид:

F = 2y1 + 3y2  (max)

-10y0 + 4y1 + y2 + y3 = 0,

-10y0 + y1 + 4y2 +y4 = 0,

    4y0 + 2y1 + y2 = 1,

yi≥0, i=1,…,4

 

Решим полученную задачу симплекс-методом. Введем дополнительную переменную, что бы получить единичный базис:

F = 2y1 + 3y2 – Mz   (max)

-10y0 + 4y1 + y2 + y3 = 0,

-10y0 + y1 + 4y2 +y4 = 0,

    4y0 + 2y1 + y2 + z = 1,

yi≥0, i=1,…,4

Составляем симплекс-таблицу.

Таблица 1.

		y0	y1	y2	y3	y4	z
Базис	План
y3	0	-10	4	1	1	0	0
y4	0	-10	1	4	0	1	0
z	1	4	2	1	0	0	1
f	0	0	-2	-3	0	0	0
M	-1	-4	-2	-1	0	0	0

 

 

 

 

 

 

Таблица 2.

		y0	y1	y2	y3	y4	z
Базис	План
y3	2,5	0	9	3,5	1	0	2,5
y4	2,5	0	6	6,5	0	1	2,5
y0	0,25	1	0,5	0,25	0	0	0,25
f	0	0	-2	-3	0	0	0
M	0	0	0	0	0	0	1

Таблица 3.

		y0	y1	y2	y3	y4	z
Базис	План
y3	1,15384615	0	5,76923	0	1	-0,5385	1,15385
y2	0,38461538	0	0,92308	1	0	0,15385	0,38462
y0	0,15384615	1	0,26923	0	0	-0,0385	0,15385
f	1,15384615	0	0,76923	0	0	0,46154	1,15385
M	0	0	0	0	0	0	1

Получаем решение:

у0 = 0,153846; y1 = 0; y2 = 0,384615; f = 1,15384615.

Тогда, возвращаясь к исходным переменным, получим:

Х1 = у1/у0 = 0; Х2 = у2/у0 = 2,5; Zmax = 1,15384615.