Расчет пружины на усталостную прочность.

    Требуется : 1. Определить максимальное τmax и минимальное τmin напряжения в проволоке пружины и вычислить коэффициент асимметрия цикла R ;

    2. Найти среднее τm и амплитудное τа напряжения цикла ;

    3. Построить в масштабе схематизированную диаграмму предельных амплитуд ( в осях τа и τm ), используя механические характеристики стали τ-1, τ0, τт ;

    4. Вычислить коэффициент запаса прочности и сравнить его с коэффициентом, полученным по диаграмме предельных амплитуд (графически).

                                                                   Решение.

    1. Определение максимального (τmax)и минимального (τmin) напряжений в проволоке пружины и вычисление коэффициента асимметрии цикла R.

    Напряжения вычисляем по формуле :

   τ=k  , где к – коэффициент, учитывающий влияние поперечной силы и неравномерность распределения напряжений от её воздействия, а также влияние деформации изгиба вследствие кривизны витков пружины.

    Этот коэффициент можно определить по формуле :

       к=  , где Сп=D/d – характеристика геометрических параметров пружины.

    В данном случае Сп=D/d=0.047/0.0039=12.1 ,

    тогда   к==1.11

    Определим величины напряжений :

          τmax=k =1.6×106 Па=1.6 МПа.

           τmin=k=0.7×106Па=0.7 МПа

    Коэффициент асимметрии цикла : R=τmin/τmax=0.7/1.6=0.44

 

    2. Найдём среднее τm и амплитудное τа напряжения цикла.

    Величины среднего и амплитудного напряжений цикла зависят от τmax и τmin и находятся по формулам :

                                τm==1.15 МПа

                                 τa==0.45 МПа

    3. Определим коэффициент запаса прочности.

    Коэффициенты запаса прочности по усталости и по пределу текучести определяются по формулам :

                                nτ=    ;   nTτ=

    где  τ-1 – предел выносливости при симметричном цикле ;

           τT – предел текучести ;

         KD= - коэффициент, учитывающий концентрацию напряжений, влияние качества обработки поверхности и абсолютных размеров поперечного сечения ;

         ψ – угловой коэффициент

                      ψ==0.16

                      KD==1.33

    Коэффициент запаса прочности по усталости :

                             nτ==601

    Коэффициент запаса по пределу текучести :

                                   nT==575

    Так как 575<601, то коэффициент запаса прочности для пружины (по текучести) n=575

 

    4. Построим в масштабе схематизированную диаграмму предельных амплитуд (в осях τа и τm).

    Зададимся прямоугольной системой координат τm и τа  с началом в точке О(0;0), в которой по оси абсцисс откладываем значения средних напряжений τm , а по оси ординат – значения амплитудных напряжений τа.

    Вычислим значения координат точки B по формулам :

  a==644 ; b==276

    На выбранной системе координат нанесём точки :

         A(0 ; τ-1/kD)  ;  B(a ; b)  ;  C(τT ; 0)  ;  M(τm ; τa)

         A(0 ; 353)  ;  B(644 ; 276)  ;  C(920 ; 0)  ;  M(1.15 ; 0.45).

    Соединим прямыми точки A с B, B c C, а через точку М из начала координат проведём луч OMN.

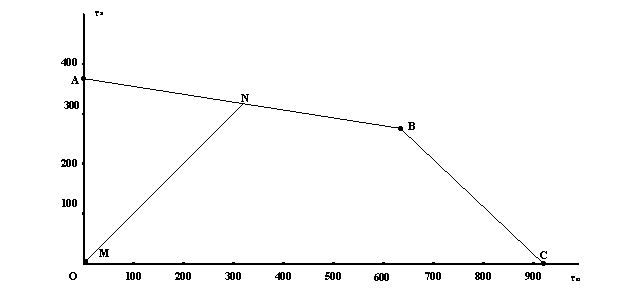
    Используя диаграмму определим коэффициент запаса прочности :

    n=ON/OM  ;  ON=106  ;  OM=0.2 ;  n=106/0.2=530