Построение эпюр изгибающих моментов и поперечных сил , подбор поперечного размера балки.

    1) Вычертить расчётные схемы, указав числовые значения размеров и нагрузок ;

    2) Вычислить опорные реакции (схема 2) и проверить их ;

    3) Составить аналитические выражения изменения изгибающего момента Mx и поперечной силы Qy на всех участков балок ;

    4) Построить эпюры изгибающих моментов Mx и поперечных сил Qy, указав значения ординат во всех характерных сечениях участков балок ;

    5) Руководствуясь эпюрами изгибающих моментов, вычертить приблизительный вид изогнутых осей балок ;

    6) Определить положения опасных сечений и из условия прочности подобрать поперечные размеры балок :

      a) для схемы 1 – круг диаметром d при допускаемом напряжении [σ]=280 МПа (сталь) ;

      б) для схемы 2 – двутавровое (ГОСТ 8239-72) при допускаемом напряжении [σ]=200 МПа (сталь).

    Дано : схема 1 - № 7 ; схема 2 - № 4 ; c/a=1.8 ; P/qa=1.8 ; m/qa2=0.8 ; a=2 м ; q=11 кН/м.

                                                                     Решение.

    а) Схема 1.

   Расчётная схема.

             P=1.8qa=1.8×11×2=39.6 кН  ;  m=0.8qa2=0.8×11×22=35.2 кН·м  ; c=1.8a=1.8×2=3.6 м.

    Эпюры поперечных сил и изгибающих моментов строим методом сечений. Определим выражения для поперечных сил и изгибающих моментов на каждом из участков балки. Балка имеет два участка. Обозначим zi – расстояние от левого конца балки до некоторого сечения.

    На участке AB : 0≤z1≤a

                         Q1=-P+qz1 ; M1=-Pz1+0.5qz12

    На участке BC : a≤z2≤c+a

                          Q2=-P+qz2 ; M2=-Pz2+m+0.5qz22

    Вычислим поперечные силы и изгибающие моменты в характерных сечениях балки.

    На участке AB : при z1=0 ;

                         QA=-P=-39.6 кН ; MA=0 кН·м.

    при z1=a ;

                        QлB=-P+qa= -39.6+11×2=-17.6 кН ;

                         MлB=-Pa+0.5qa2=-39.6×2+0.5×11×22= -57.2 кН·м.

    На участке BC : при z2=a ; QпрB=-P+qa=-39.6+11×2=-17.6 кН ;

                          MпрB=-Pa+m+0.5qa2=-39.6×2+35.2+0.5×11×22= -22 кН·м.                        

    при z2=a+c ; QC=-P+q(a+c)=-39.6+11×(2+3.6)=22 кН ;

                      MС=-P(a+c)+m+0.5q(c+a)2=-39.6×(2+3.6)+35.2+0.5×11×(3.6+2)2= -14.1 кН·м.

    На участках AB и BC эпюра Q изменяется по линейному закону (её эпюра представляет собой наклонную линию), а эпюра М ограничена параболой, которая имеет экстремум на участке BC, так как эпюра Q меняет свой знак на этом участке. Так в данной задаче нас интересуют только максимальные значения в пределах участков (по абсолютной величине), то для построения эпюры на участке AB достаточно двух точек, а на участке BC необходимо три точки. (Наибольшим будет одно из граничных значений).

    Найдём сечение, где действует экстремальный момент из условия :

                           Q2=-P+qz0

    Отсюда :  z0=P/q=39.6/11=3.6 м

    Найдём значение экстремального момента :

                              Mэкс=-Pz0+m+0.5qz02=-39.6×3.6+35.2+0.5×11×3.62=-36.1 кН·м нобходимо три точки                                                

    По полученным данным строим эпюры Q и М. Для этого отложим перпендикулярно к оси абсцисс в удобном для пользовании масштабе вычисленные значения Q и М для граничных сечений участков и соединим концы полученных ординат линиями, соответствующими законам изменения Q и М. При этом положительные ординаты эпюры Q будем откладывать вверх, а отрицательные – вниз от оси абсцисс ; ординаты же эпюры М будем откладывать со стороны растянутых волокон.

    Построим теперь изображение примерного вида изогнутой оси балки. Поскольку наши построения носят приблизительный характер, то основой для проведения такой линии будут являться следующие положения : кривизна балки на участках соответствует расположению эпюр изгибающих моментов, т.е. , так как эпюра Мx построена на нижних волокнах (в данном случае они растянуты, то балка будет изгибаться вниз. В точке заделки поворот сечения отсутствует, следовательно, линия изогнутой оси балки должна выходить под прямым углом (в данном случае, к вертикали). Построенная с учётом сказанного упругая линия консольной балки изображена на рисунке. 

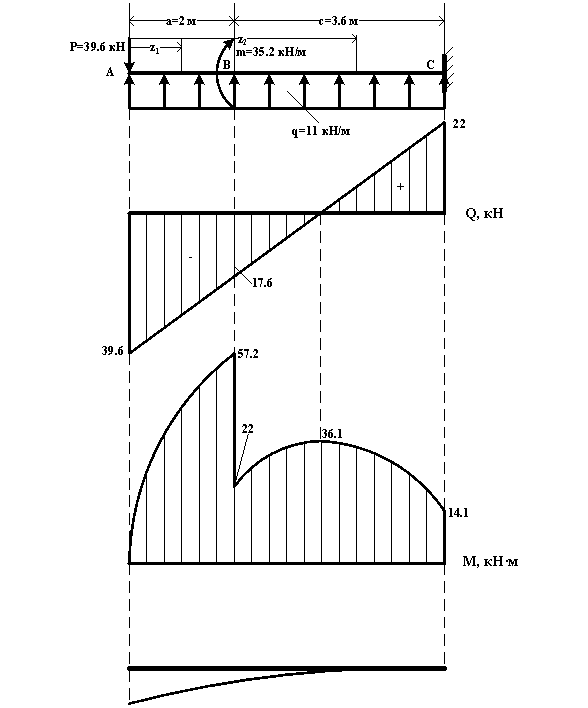
    Подберём размеры круглого сечения методом допускаемого напряжения, т.е. в рассмотрение следует принимать лишь сечение балки, в котором действует наибольший по абсолютной величине изгибающий момент. В нашем примере опасным является сечение B, в котором Mmax=57.2 кН·м.

    Круглое сечение стальной балки подбираем из условия прочности при допускаемом напряжении [σ]=280 МПа :

                                    σ=Mmax/Wx=[σ]

    Откуда находим требуемый момент сопротивления сечения балки при изгибе :

                   Wx=57.2×103/(280×106)=204.3×10-6 м3=204.3 см3

    Момент сопротивления круглого сечения относительно нейтральной оси X имеет вид :

                   Wx=0.1d3

    Тогда :    d==12.7 см. Принимаем d=13 см.

  б) Схема 2.

  Расчётная схема.

       P=1.8qa=1.8×11×2=39.6 кН  ;  m=0.8qa2=0.8×11×22=35.2 кН·м  ; c=1.8a=1.8×2=3.6 м.

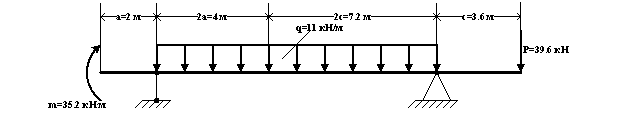
    Для определения опорных реакций воспользуемся уравнениями статики.

               ΣmC=0  ; -Pc-RB(2a+2c)+0.5q(2a+2c)2-m=0  , откуда

      RB==45.73 кН

               ΣmB=0  ;  -P(2a+3c)-0.5q(2a+2c)2+RC(2a+2c)-m=0 , откуда

      RC==117.07 кН.

    Сделаем проверку. Для этого составим уравнение проекций сил на вертикальную ось.

                  ΣY=-P+RB-q(2a+2c)+RC=-39.6+45.73-11×(4+7.2)+117.07=162.8-162.8=0

    Реакции вычислены верно. Горизонтальная составляющая реакции в опоре C равна нулю и на рисунке не показана.

    Балка имеет три участка. Запишем выражения для поперечных сил и изгибающих моментов на каждом из участков.

    Участок AB (ход слева) ; 0≤z1≤a ; Q1=0 ; M1=m

    Участок BC (ход слева) ; a≤z2≤3a+2c ; Q2=RB-q(z2-a) ; M2=m+RB(z2-a)-0.5q(z2-a)2

    Участок СD (ход справа) ; 0≤z3≤c ; Q3=P ; M3=-Pz3

    Определим значения Qy и Мx в характерных точках балки.

    Участок AB : z1=0 ; QA=0 кН ; MA=m=35.2 кН∙м.

                            z1=a ; QлB=0 кН ; MлB=m=35.2 кН·м.

    Участок BC : z2=a ; QпрB=RB=45.73 кН ; MпрB=m=35.2 кН·м.

                            z2=3a+2c ; QлC=RB-q(2a+2c)=39.6-11×(4+7.2)=-83.6 кН ;

           MлC=m+RB(2a+2c)-0.5q(2a+2c)2=35.2+45.73×(4+7.2)-0.5×11×(4+7.2)2=-142.5 кН·м.

    Участок CD : z3=с ; QпрC=P=39.6 кН ; MпрC=-Pc=-39.6×3.6=-142.5 кН·м.

                            z3=0 ; QD=P=39.6 кН ; MD=0

    На участке BC эпюра М ограничена параболой, которая имеет экстремум в сечении, где поперечная сила равна нулю. Найдём координату этого сечения из условия :

Q2=RB-q(z0-a)=0 , откуда  z0=RB/q+a=39.6/11+2=5.6 м. Тогда экстремальный момент : Mэкс=m+RB(z0-a)-0.5q(z0-a)2=35.2+45.73×(5.6-2)-0.5×11×(5.6-2)2=128.5 кН·м.

    По результатам расчета строим эпюры Q и М. В той же последовательности, что и для консольной балки.

    Построим изображения примерного вида изогнутой оси балки. В отличии от первого случая здесь имеются две характерные точки (опоры B и C), в которых перемещения равны нулю. Так же имеется точка перегиба, где меняется направление изгиба оси балки (в сечении с изгибающим моментом равным нулю).

    Номер двутавра для балки подбираем из условия прочности при изгибе и допускаемом напряжении [σ]=200 МПа.

                            σ=Mmax/Wx=[σ]

    В нашем случае Mmax=142.5 кН·м

    Требуемый момент сопротивления Wx=142.5×103/(200×106)=712.5×10-6 м3=712.5 см3

    По сортаменту (ГОСТ 8239-72) выбираем двутавр №36 с Wx=743 см3

              σ=Mmax/Wx=142.5×103/(743×10-6)=192×106 Па=192 МПа<[σ]=200 МПа

    Прочность балки обеспечена.