Примеры решенных задач по математике - Контрольная 1

                                                                         № 324

    Выяснить, сходится, ли заданный ряд.

  Дано :

                                                                      Решение.

    Для исследования сходимости ряда, применим признак Даламбера.

    Зная n-й член ряда, находим следующий за ним (n+1)-й член, заменяя в выражении n-го члена n через n+1. затем ищем предел отношения последующего члена un+1 к предыдущему un при неограниченном возрастании n :

            

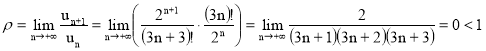
    Здесь ρ<1. Поэтому согласно признаку Даламбера данный ряд сходится.

    Ответ : ряд сходится.

 

                                                                          № 334

    Определить область сходимости данного ряда.

    Дано :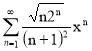

                                                                        Решение.

    Имеем : un= 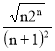 ;  un+1=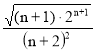

   Радиус сходимости R находим по формуле : R=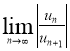

    Тогда R=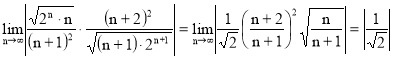

 

    Следовательно, на основании теоремы Абеля, исходный ряд абсолютно сходится в интервале

  или  . Исследуем сходимость ряда на концах интервала ходимости.

    Пусть x= -. Тогда получим ряд : 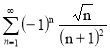. Этот знакочередующийся ряд сходится по признаку Лейбница.  В самом деле,

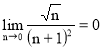    ;  , т.е., члены ряда убывают по абсолютной величине.

    Пусть x=. Тогда, получим ряд : 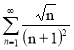. Этот ряд с положительными членами сходится. Так как каждый его член, начиная с первого меньше соответствующего члена бесконечной геометрической прогрессии , которая сходится (так как её знаменатель 1/2<1). А, значит, по признаку сравнения сходится и исходный ряд. Итак, заданный ряд сходится в области                                 Ответ : x∈

 

 

 

                                                                         № 344

    Разложить функцию f(x) в ряд Фурье в указанном интервале. Выписать полученный ряд и три первых члена разложения отдельно. Построить графики функций f(x) и её приближения

  S2(x)=

    Дано : f(x)= в интервале (-1 ; 1).

                                                                  Решение.

    Ряд Фурье функции f(x), определённой на отрезке [-l ; l], l>0

                                               (1)

    Данная функция f(x)= – чётная, вследствие чего все коэффициенты bn=0, а коэффициенты an вычисляются по формуле :

      an=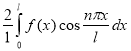, n=0,1,2,…                                    (2)

    По формуле при l=1, получаем (в интервале функция определяется формулой

   f(x)=x – 1) :

    an=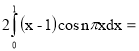(интегрируем по частям)=

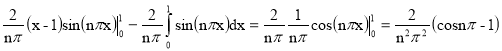= , при n=1, 2, 3, …, n≠0

    При n чётном cos(nπ)=1 и an=0 ; при n нечётное cos(nπ)=-1 и an= , k=1, 2, 3, …

    При n=0 полученное здесь выражение для an непригодно, вследствие чего коэффициент а0 вычисляем отдельно, полагая n=0 в формуле (2) :

   a0=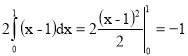

    Подставляя найденные коэффициенты в ряд Фурье (1), получим

  S(x)=

    Выпишем три первых члена : u0= ; u1= ; u2=

    Построим графики функций : f(x)= и S2(x)=

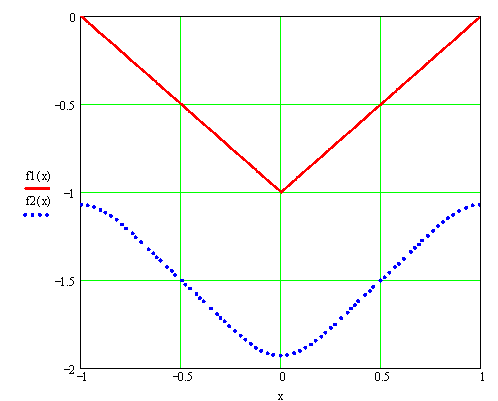
    Ответ : S(x)=

 

 

                                                                         № 354

    Найти решение дифференциального уравнения, удовлетворяющее заданным начальным условиям, применяя метод операционного исчисления. Сделать проверку найденного решения.

  Дано : y//+2y/-3y=et  , y(0)=0  ,  y/(0)=0

                                                                          Решение.

    Заданное уравнение – есть линейное неоднородное дифференциальное уравнение второго порядка. Его решение y=y(t) будем искать операционным методом. По таблице изображений находим лапласовы изображения входящих в уравнение слагаемых.

  L[y(t)]=Y(p) ; L[y//(t)]=p2Y(p)-py(0)-y/(0)=p2Y(p) ;

  L[y/(t)]=pY(p)-py(0)=pY(p)

  L[et]==

    Подставляя найденные изображения в исходное уравнение, получаем изображающее уравнение, которое всегда является линейным алгебраическим уравнением относительно Y(p).

   p2Y(p)+2pY(p)-3Y(p)=

  Y(p)=

Разлагаем дробь в правой части на простейшие дроби.

  , откуда

        1=A(p2+3p-p-3)+Bp+3B+C(p2-2p+1)=Ap2+2Ap-3A+Bp+3B+Cp2-2Cp+C=

=p2(A+C)+p(2A+B-2C)-3A+3B+C

    Приравнивая коэффициенты при одинаковых степенях x , получим систему уравнений для определения коэффициентов A, B и С.

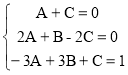  ; откуда A= ; B= ; C=

     Следовательно, Y(p)=

    Переходим к оригиналам Y(p)→y(t)

      ;   ; и окончательно получаем

         y(t)=

    Сделаем проверку. Для этого найдём y//(t) и y//(t)

      y/(t)= ;

        y//(t)=

   Подставим y(t), y/(t) и y//(t) в исходное уравнение.

   

    Ответ : y(t)=

                                                                        № 364

    Вычислить криволинейный интеграл. Выполнить чертёж дуги кривой.

    Дано : 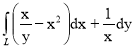, где L – дуга кривой y=x2 от точки (1 ; 1) до точки (2 ; 4)

                                                                              Решение.

    Пользуясь , уравнением линии интегрирования, преобразуем криволинейный интеграл в обыкновенный интеграл с переменной x, затем вычисляем его

             y=x2  ;  dy=2xdx

    =

    =

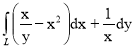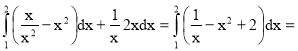
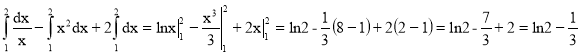
  Выполним чертёж дуги кривой.

   

 

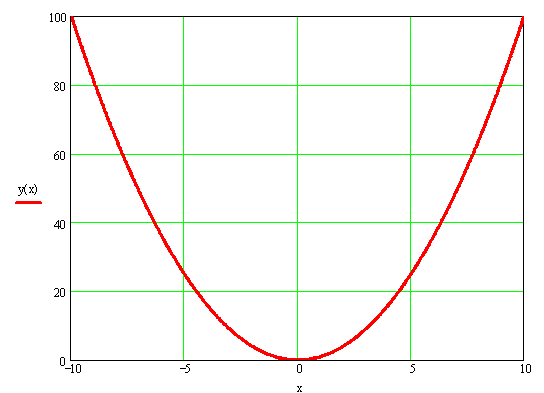
                                                                         № 374

    Найти поток векторного поля в направлении нормали через поверхность треугольника S, высекаемого координатными плоскостями из плоскости, проходящей через точку P перпендикулярно вектору . Сделать чертёж.

    Дано : =(x-2y+z) ; (1 ; 2 ; 2) ; P(0 ; 2 ; 0 )

                                                                       Решение.

    Уравнение плоскости, проходящей через точку М0(x0 ; y0 ; z0) перпендикулярно нормальному вектору (A, B, C) имеет вид :

              A(x-x0)+B(y-y0)+C(z-z0)=0

    Составим уравнение заданной поверхности S (плоскости, проходящей через точку P перпендикулярно вектору ).

   (x-0)+2(y-2)+2(z-0)=0  ;  x+2y-4+2z=0  ;  x+2y+2z-4=0

    Следовательно, поверхность S есть часть плоскости  x+2y+2z-4=0.

    Последнее уравнение запишем в форме уравнения в отрезках

                    

    Отсюда, отрезки координатных осей, отсекаемые плоскостью от начала координат О, равны x=4 ; y=2 ; z=2. Строим поверхность S. Треугольник ABC есть искомая поверхность S с нормальным вектором (1; 2; 2)

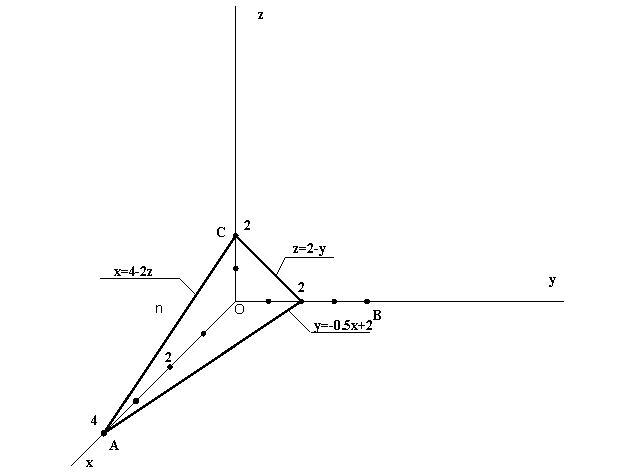
    Вычислим поток векторного поля.

    По условию P(x,y,z)=x-2y+z ; Q(x,y,z)=0 ; R(x,y,z)=0

    По формуле, получаем :

  П= =

====

==

==

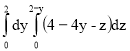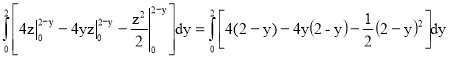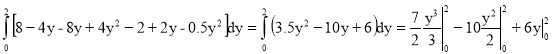= =4/3

    Ответ : П=4/3.

 

 

 

                                                                        № 384

    Проверить, является ли векторное поле соленоидным и потенциальным. В случае потенциальности поля найти его потенциал.

    Дано : (10x+3yz ; 10y+3xz ; 10z+3xy)

                                                                Решение.

     Векторное поле является потенциальным, если

  rot=

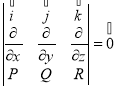
    находим ротор заданного векторного поля :

  rot= =-

-+=

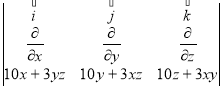=[3x-3x]-[3y-3y]+[3z-3z]=

    Следовательно, поле является потенциальным.

    Потенциал u(x,y,z) потенциального векторного поля при переходе из точки A(x0,y0,z0) в точку B(x,y,z) находится по формуле.

  U(x,y,z)=    =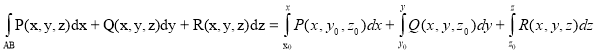

Так как поле является потенциальным, то найдём его потенциал.

    U(x,y,z)==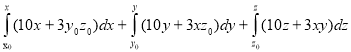

==

==

= 5x2+5y2+5z2+3xyz-5x02-3x0y0z0-5y02-5z02=5(x2+y2+z2)+3xyz+C0

где C0=-5x02-5y02-5z02-3x0y0z0

    Поле является соленоидным, если

             div=

    Находим дивергенцию поля :

  div=

    Ответ : поле потенциально и не соленоидально.

       U(x,y,z)= 5(x2+y2+z2)+3xyz+C0   ;  C0=-5x02-5y02-5z02-3x0y0z0