Контрольная по теории вероятности.
Ниже приведены условия и решения задач. Закачка решений в формате doc начнется автоматически через 10 секунд.
№ 1 Брошены две игральные кости, на каждой из которых могут выпасть цифры от 1 до 6. Найти вероятность того, что сумма выпавших на обеих костях очков равна 5, а произведение 4.
Решение.
Рассмотрим событие А – сумма выпавших на обеих костях очков равна 5.
Вероятность события А вычислим с помощью классического определения вероятности
![]()
где n – общее число равновозможных элементарных исходов испытания; m – число элементарных исходов, благоприятствующих появлению события A.
Общее число различных случаев равно
![]()
В сумме число 5 можно получить 4 способами: (1;4), (4;1), (2;3), (3;2)
Тогда искомая вероятность равна
![]()
Рассмотрим событие В – произведение выпавших на обеих костях очков равно 4.
Вероятность события В вычислим с помощью классического определения вероятности .
Общее число различных случаев равно
![]()
Произведение очков, равное 4 можно получить 3 способами:(1;4), (4;1), (2,2).
Тогда искомая вероятность равна
![]()
Ответ: ![]() ,
,![]()
№ 11 Даны независимые случайные величины X и Y. Найти математическое ожидание произведения ![]() и суммы
и суммы ![]() дискретных случайных величин. Вычислить дисперсию D(X) и среднее квадратическое отклонение
дискретных случайных величин. Вычислить дисперсию D(X) и среднее квадратическое отклонение ![]() .
.
|
хi |
1 |
2 |
|
yi |
0,5 |
1 |
|
pi |
0,2 |
0,8 |
|
qi |
0,3 |
0,7 |
Решение.
Так как X и Y – независимые величины, то мы имеем
![]()
![]()
Математические ожидания величин X и Y найдем по формулам
![]()
![]()
Тогда
![]()
![]()
Дисперсию D(X) найдем по формуле
![]()
![]()
Тогда
![]()
Среднее квадратическое отклонение ![]() найдем по формуле
найдем по формуле
![]()
Ответ: ![]() ,
,![]() ,
, ![]() ,
, ![]()
№21 Задана непрерывная случайная величина Χ функцией распределения F(х). Требуется: 1) найти плотность распределения вероятностей f(x) ; 2) схематично построить графики функций f(x) и F(х);
3) найти математическое ожидание, дисперсию и среднеквадратическое отклонение случайной величины Х; 4) найти вероятность того, что Х примет значение из интервала (![]() ).
).
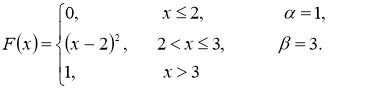
Решение.
1) Плотность распределения вероятностей f(x) будем искать как производную от функции распределения ![]()
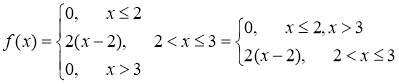
2) Построим график функции f(x)
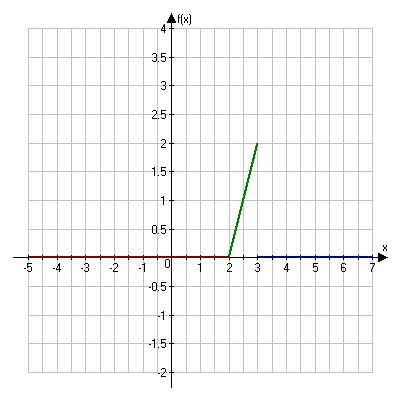
Построим график функции F(x)
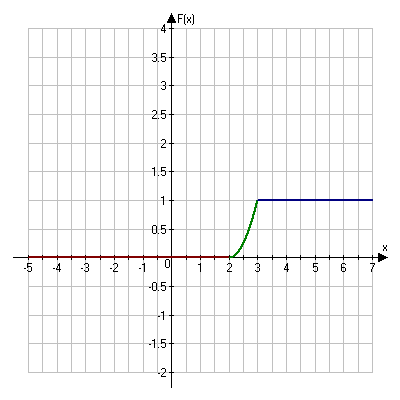
3) Вычислим математическое ожидание ![]()
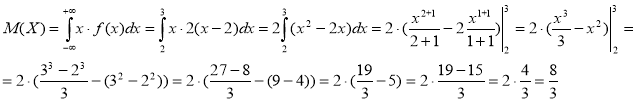 Дисперсию вычислим по формуле
Дисперсию вычислим по формуле ![]() , где
, где
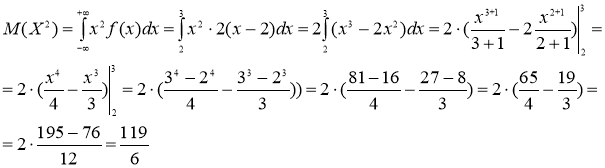
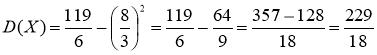
Среднеквадратическое отклонение равно
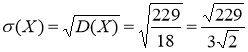
4) Вероятность попадания на интервал (![]() ) будем искать по формуле
) будем искать по формуле
![]()
![]()
Ответ: 1) 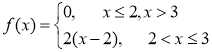 ,3)
,3) ![]()
![]()
![]()
4) ![]()
№31 Заданы среднее квадратическое отклонение σ нормально распределенной случайной величины Х, выборочная средняя ![]() и объем выборки n. Требуется: 1) найти доверительный интервал для оценки неизвестного математического ожидания а с доверительной вероятностью
и объем выборки n. Требуется: 1) найти доверительный интервал для оценки неизвестного математического ожидания а с доверительной вероятностью ![]() =0,95; 2) принимая
=0,95; 2) принимая ![]() , написать теоретическую плотность распределения вероятностей и схематично построить ее график; 3) следуя правилу “трех сигм”, определить приближенно максимальное и минимальное значения случайной величины Х; 4) оценить вероятность того, что Х примет значение, превышающее
, написать теоретическую плотность распределения вероятностей и схематично построить ее график; 3) следуя правилу “трех сигм”, определить приближенно максимальное и минимальное значения случайной величины Х; 4) оценить вероятность того, что Х примет значение, превышающее ![]()
![]()
Решение.
1) Для определения доверительного интервала для математического ожидания воспользуемся формулой
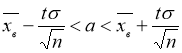
По таблице функции Лапласа из соотношения
![]()
найдем ![]() .
.
Определим точность оценки
![]()
Следовательно, доверительный интервал будет
![]()
![]()
2) Так как CВ Х распределена нормально, то плотность распределения будет иметь вид
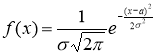
Так как мы принимаем ![]() и по условию
и по условию ![]() , то
, то
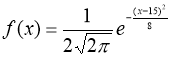
Постоим график ![]()
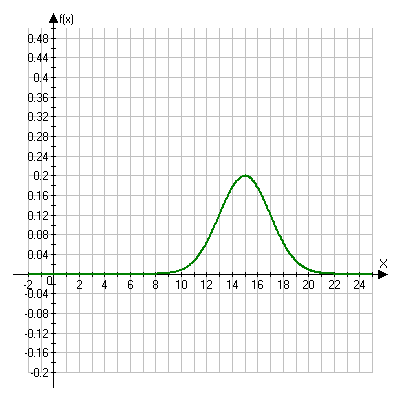
3) По правилу “трех сигм” почти все значения случайной величины Х лежат в промежутке
![]()
![]()
![]()
4) Для нормального распределения функция распределения запишется
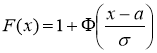
Вероятность попадания на отрезок ![]() будем искать по формуле
будем искать по формуле
![]()
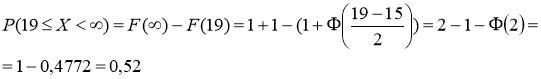
Ответ: 1) ![]() , 2)
, 2) 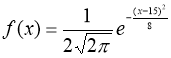 ,
,
3) ![]() ,
,![]() , 4)
, 4) ![]()
№41 Отдел технического контроля проверил n партий изделий и установил, что число Х нестандартных изделий в одной партии имеет следующее эмпирическое распределение, сведенное в таблицу, где ![]() - число нестандартных изделий в одной партии;
- число нестандартных изделий в одной партии; ![]() - число партий, содержащих
- число партий, содержащих ![]() нестандартных изделий. Требуется при уровне значимости
нестандартных изделий. Требуется при уровне значимости ![]() проверить гипотезу о том, что случайная величина Х распределена по закону Пуассона. Использовать критерий согласия Пирсона
проверить гипотезу о том, что случайная величина Х распределена по закону Пуассона. Использовать критерий согласия Пирсона ![]() .
.
n=250; α =0,05
|
|
0 |
1 |
2 |
3 |
4 |
5 |
6 |
|
|
101 |
91 |
44 |
10 |
2 |
1 |
1 |
Решение.
Находим выборочную среднюю
![]()
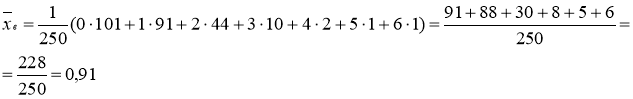
В качестве оценки параметра ![]() распределения Пуассона
распределения Пуассона 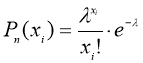
выберем полученное значение выборочного среднего ![]()
Проверим гипотезу о том, что случайная величина Х распределена по закону Пуассона, пользуясь критерием Пирсона
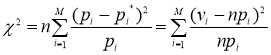 .
.
Расчет теоретических частот ![]()
![]()
![]()
![]()
![]()
![]()
![]()
![]()
Расчеты приведем в таблице
|
|
|
|
|
|
0 |
101 |
0,405 |
101,25 |
|
1 |
91 |
0,368 |
92 |
|
2 |
44 |
0,168 |
42 |
|
3 |
10 |
0,051 |
12,75 |
|
4 |
2 |
0,012 |
3 |
|
5 |
1 |
0,002 |
0,5 |
|
6 |
1 |
0,0003 |
0,07 |
Малочисленные частоты ![]() можно объединить, и при этом объединить соответствующие им теоретические частоты.
можно объединить, и при этом объединить соответствующие им теоретические частоты.
|
|
|
|
|
101 |
101,25 |
0,0006 |
|
91 |
92 |
0,011 |
|
44 |
42 |
0,095 |
|
10 |
12,75 |
0,593 |
|
4 |
3,57 |
0,052 |
|
|
Сумма |
0,752 |
Получили ![]() . Найдем число степеней свободы
. Найдем число степеней свободы ![]() . Так как проверяется гипотеза о распределении Пуассона, то
. Так как проверяется гипотеза о распределении Пуассона, то ![]() .
. ![]() , так как после объединения малочисленных частот осталось 5 строк.
, так как после объединения малочисленных частот осталось 5 строк.
![]()
По таблице критических точек распределения ![]() по уровню значимости
по уровню значимости ![]() и числу степеней свободы k = 3 находим критическую точку
и числу степеней свободы k = 3 находим критическую точку
![]() 7,8
7,8
Так как ![]() , то гипотеза о том, что CВ Х распределена по закону Пуассона принимается.
, то гипотеза о том, что CВ Х распределена по закону Пуассона принимается.
Ответ: гипотеза верна
№ 51 В процессе эксплуатации ЭВМ возникают неисправности (сбои). Поток сбоев считаем простейшим. Среднее число сбоев за сутки равно m. Найти вероятности следующих событий:
А - за n суток нет ни одного сбоя;
В – за одни сутки будет хотя бы один сбой;
С – за неделю произойдет не менее k сбоев.
![]()
Решение.
Решение задачи будем искать по формуле
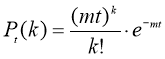
Где m- среднее число сбоев за сутки, к- количество сбоев за сутки, t- количество суток.
Рассмотрим событие А - за 2 суток (t=2)нет ни одного сбоя (к=0). Тогда вероятность этого события равна
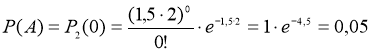
Вероятность события В – за одни сутки (t=1) будет хотя бы один сбой найдем как вероятность противоположного события ![]() - за сутки ни одного сбоя. Воспользуемся свойством вероятности противоположных событий
- за сутки ни одного сбоя. Воспользуемся свойством вероятности противоположных событий
![]()
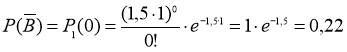
Тогда
![]()
Найдем вероятность того, что за неделю произойдет не менее 3 сбоев (событие С). Воспользуемся свойством вероятности противоположных событий
![]()
Где событие ![]() - за неделю произошло 0,1,2 сбоев. Найдем вероятность события
- за неделю произошло 0,1,2 сбоев. Найдем вероятность события ![]()
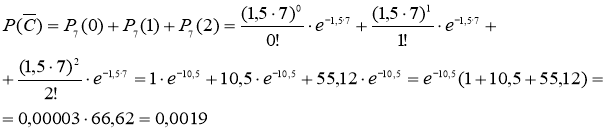
Тогда
![]()
Ответ: ![]() ,
, ![]() ,
,![]()
№61 Задана матрица
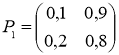
вероятностей перехода дискретной цепи Маркова из i-го состояния в j-ое за один шаг (i, j=1, 2). Распределение вероятностей по состояниям в начальный момент t=0 определяется вектором ![]() =(0,4; 0,6). Найти:
=(0,4; 0,6). Найти:
1) матрицу Р2 перехода цепи из состояния i в состояние j за два
шага;
2) распределение вероятностей по состояниям в момент t=2;
3) вероятность того, что в момент t=1 состоянием цепи будет i=2;
4) стационарное распределение.
Решение.
1) Для дискретной цепи Маркова в случае ее однородности справедливо соотношение
![]()
где Р1 – матрица переходных вероятностей за один шаг;
Рn - матрица переходных вероятностей за n шагов;
Найдем матрицу Р2 перехода за два шага
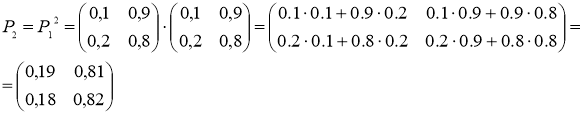
2) Распределение вероятностей по состояниям в момент t=2 определяется формулой
![]() ,
,
так как из состояния в момент времени t=0 в состояние в момент времени t=2 система переходит за два шага.
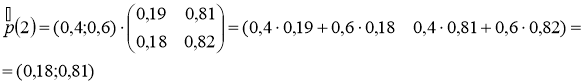
3) Распределение вероятностей по состояниям в момент t=1 определяется формулой
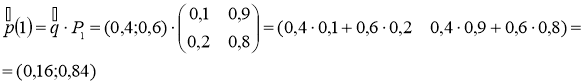
Вероятность того, что в момент t=1 состоянием цепи будет i=2 равна
р2(1)=0,84.
4) Для определения стационарного распределения вероятностей составляем систему уравнений
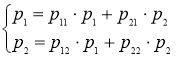
Где ![]() - элементы матрицы Р1. К данной системе добавляется еще и условие нормировки
- элементы матрицы Р1. К данной системе добавляется еще и условие нормировки ![]() В итоге получим
В итоге получим
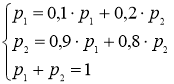 ,
, 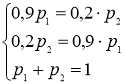 ,
, 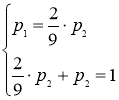 ,
, 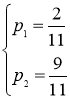
Следовательно, 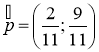 - стационарное распределение вероятностей
- стационарное распределение вероятностей
Ответ: 1)  , 2)
, 2) ![]() , 3) р2(1)=0,84,
, 3) р2(1)=0,84,
4) 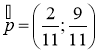
№81 Найти спектральную плотность стационарной случайной функции Х(t), если ее корреляционная функция имеет вид
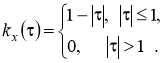
Решение:
Спектральную плотность будем находить по формуле
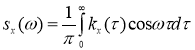
Учитывая, что ![]() в интервале (0,1), имеем
в интервале (0,1), имеем
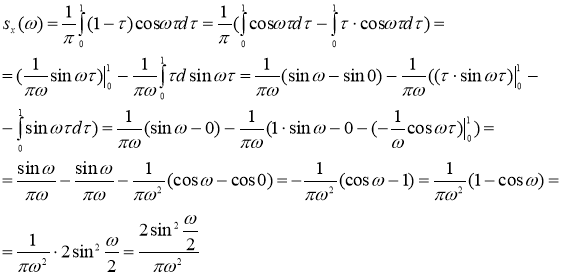 Ответ:
Ответ: 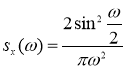
91.На вход линейной стационарной динамической системы, описываемой данным дифференциальным уравнением, подается стационарная случайная функция Х(t) с математическим ожиданием mx и корреляционной функцией kx(τ). Найти: 1) математическое ожидание; 2) дисперсию случайной функции Y(t) на выходе системы в установившемся режиме.
![]()
Решение.
1) Найдем математическое ожидание, используя формулу:
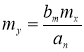
В данном случае ![]() (коэффициент при X(t) ),
(коэффициент при X(t) ), ![]() (коэффициент при Y(t), mx = 3 по условию
(коэффициент при Y(t), mx = 3 по условию
![]()
2) Найдем спектральную плотность
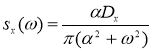
где ![]() ,
, ![]() =2
=2
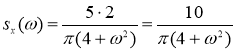
Найдем передаточную функцию, для чего напишем заданное уравнение в операторной форме:
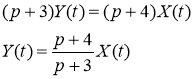
Cледовательно, передаточная функция:
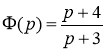
Найдем частотную характеристику, для чего заменим в передаточной функции аргумент р на iw:
![]()
Найдем спектральную плотность выходной функции, для чего умножим спектральную плотность входной функции на квадрат модуля частотной характеристики:
![]()
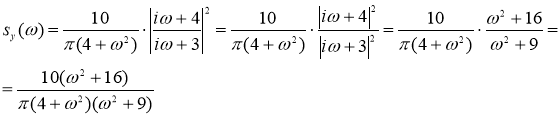
Найдем искомую дисперсию:
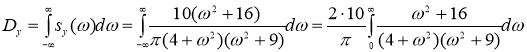
Представим дробь 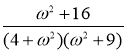 в виде суммы дробей
в виде суммы дробей
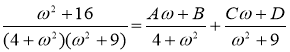
Приведя правую часть последнего равенства к общему знаменателю и приравняв числители дробей, получим тождество:
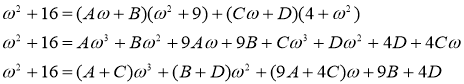
Найдём искомые коэффициенты из системы:
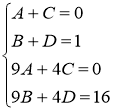
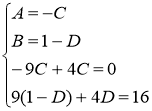
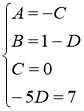
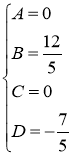
Тогда
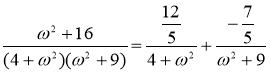
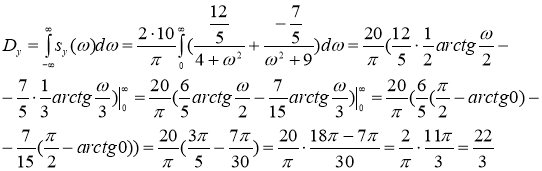
Ответ: ![]() ,
, ![]()
1
Имя файла: Mat3.doc
Размер файла: 447 Kb
Если закачивание файла не начнется через 10 сек, кликните по этой ссылке